مقاله

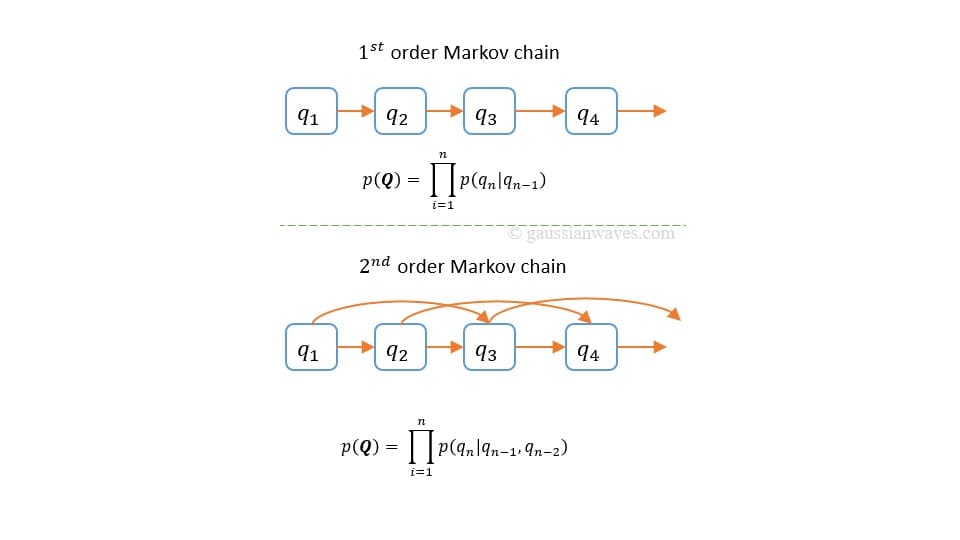
یکی از مفاهیمی که می توان گفت اساس خیلی از راه حل های مهندسی بر پایه آن است، زنجیره مارکوف است. خیلی از کارهایی که ما انجام می دهیم ممکن است به گذشته مربوط باشد، ولی تا چه میزان؟ هر چه طول وابستگی به گذشته بیشتر باشد، به تبع حالتهای مختلفی امکان وقوع دارند. فرض کنید که سه پدیده که یکی پس از دیگری قرار است اتفاق بیافتد را می خواهیم بررسی کنیم. اگر مباحث مربوط به احتمالاتشان را مورد مطالعه قرار دهیم، اگر این سه پدیده به هم وابستگی داشته باشند، لازم است توزیع joint را پیدا کنیم. فرض کنید که هر کدام از این سه، 5 حالت متفاوت داشته باشند. پس تعداد کل حالت ها برای توصیف تابع احتمال می شود پنج به توان سه. یعنی برای سه متغیر این تعداد حالت، که زیاد است، وجود دارد. حال اگر فرض کنیم که هر کدام از این متغیرها مستقل هستند و به متغیر قبلی وابسته نیستند، مارکوف مرتبه اول، می توان گفت که احتمال قبلی که تعداد حالات زیادی برای بررسی داشت تبدیل می شود به ضربِ سه تابع احتمال جدا از هم که هر یک پنج حالت دارند. برای فهم بهتر، در حالت اولیه برای توصیف کل احتمال نیاز است که پنج به توان سه حالت را بررسی کنیم ولی برای حالت دوم می توان کل تابع احتمال را با دانستن احتمال سه توزیعِ marginal که هر یک پنج حالت دارند، توصیف کرد. به عبارتی مساله ای که حالاتش خیلی زیاد می شد را با یک فرض ساده به یک مساله ساده تر تبدیل کردیم. در اطراف ما پدیده های مختلفی هستند که گذشته برایشان چندان اهمیت ندارد. هر وضعیت شطرنجی که داده شود، در آن لحظه مهم نیست گذشته چه کرده ایم، حرکت کنونی مهم است. این روش ساده در جای جایِ هوش مصنوعی استفاده شده است. خوبی مارکوف این است که شما می توانید حتی پدیده هایی که به گذشته وابسته هستند را هم دخیل کنید. به این شکل که در state کنونی هر چه که از گذشته لازم دارید را قرار می دهید تا state کنونی و بعدی به هم وابسته نباشند و در state کنونی اطلاعات مناسب وجود داشته باشد.