مقاله

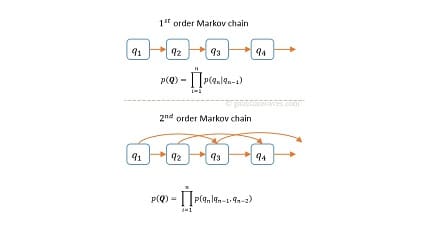
پیش از این در مورد group theory صحبت کرده بودیم. در این پست در مورد بحثی که در یادگیری عمیق خیلی وابسته به نظریه گروه است، صحبت می کنیم. ذکر کردیم که در نظریه گروه به دنبال بررسی تقارن هستیم. حال چرا این موضوع اهمیت دارد؟ در طبیعت خیلی از اشیا و موجودات زنده، نظیر گیاهان و حشرات، دارای تقارن هستند. به هر حال هر موجودی DNA دارد و ساختارهای متقارن نیاز به اطلاعات کمتری برای انکد شدن دارند. این موضوع در یادگیری عمیق و یادگیری فیلترها می تواند بسیار کمک کننده باشد. در هر حال قبلا توضیح داده بودیم که شبکه های کانولوشنی در چه زمینه هایی ضعف دارند. یکی از این ضعف ها، ضعف در چرخش بود. یعنی اگر یک جسم را می چرخاندیم، شبکه امکان داشت که خوب کار نکند. علت این موضوع این است که با چرخش، فیچرمپ استخراج شده با حالت عادی متفاوت است. اگر شبکه در مرحله data augmentation فیچرمپ مشابه ندیده باشد، به سختی می افتد. حال آیا می توانیم با توجه به وجود تقارن و یکسری ویژگی که در اجسام تکرار می شوند عملیاتِ کانولوشنیِ جدیدی ارایه کنیم که ویژگیهایی را در خود داشته باشد که تقارن لحاظ شود یا پس از چرخش که ماهیت اجسام به صورت کلی تغییر نمی کند، فیچرمپ یکسان باشد؟ پاسخ مثبت است و مباحث این زمینه در مورد Group Equivariant Deep Learning است. در این زمینه مقالات جالب بسیاری در سالهای اخیر چاپ شده اند که می توان به ساخت GCNN ها اشاره کرد.