در جبر خطی بحثی وجود دارد در مورد بردارهای پایه. اگر ساده بگوییم، اگر دو بردار داشته باشیم، با این دو بردار می توان تمامی بردارهایی که در (ابر) صفحه دربرگیرنده این دو بردار قرار دارند را بسازیم، به شرطی که دو بردار موازی نباشند. وقتی دو بردار را از فضای دو بعد به فضای مثلا سه بعد می بریم، همچنان دو بردار داریم؛ یعنی نمی توانیم با این دو بردار کل فضای سه بعدی را توصیف کنیم. به عبارتی با این دو بردار می توان یک خط، در صورت توازی دو بردار، یا یک صفحه را در فضای سه بعد توصیف کرد.
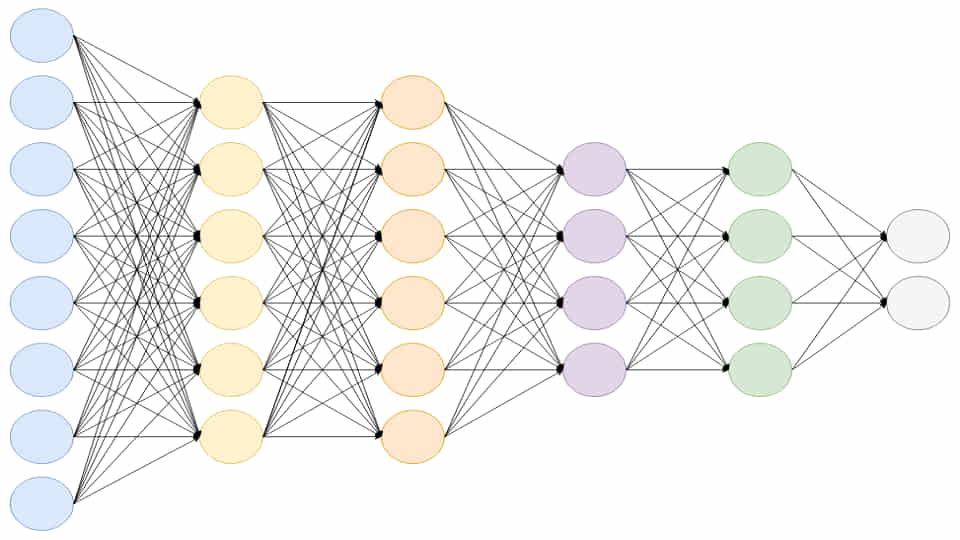
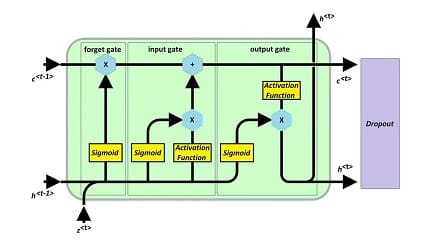
در لایه های تمام اتصال، وقتی از یک لایه به لایه بعدی می رویم، قبل از اعمال تابع فعالیت لایه متاخر، کاری که انجام می دهیم این است که تعدادی بردار را از یک بعد مشخص به بعدی دیگر می بریم. اگر در لایه ای ده و در لایه بعدی بیست نورون داشته باشیم، گویا بردارها را از فضای ده بعدی به بیست بعدی می بریم.
اگر از تابع فعالیت خطی استفاده کنیم، با توجه به مورد ذکر شده در جبر خطی، قدرت خاصی اضافه نشده ولی با اعمال توابع غیر خطی به عنوان تابع فعالیت، می توان قدرت یادگیری توابع پیچیده را داشت.